5 mysterious programming problems

5 mysterious programming problems

Here are five mysterious programming problems and their solutions.

1. Fib^2

fib(20) is only 10946, so we can just figure out fib(i). Then figure out fib of fib(i)

#include<iostream>
#include<cstring>

using namespace std;

const int MOD = 1000000007;

long long f[1000100];

int main(){
    int n;
    cin>>n;
    f[0] = f[1] = 1;
    for(int i=2; i<=n; ++i)
        f[i] = (f[i-1] + f[i-2]) %MOD;
    int t = f[n];
    for(int i=n+1; i<=t; ++i)
        f[i] = (f[i-1] + f[i-2]) %MOD;
    printf("%lld\n", f[t]);
    return 0;
}

2. The sustainable development of the research group

It’s easy to think of a greedy strategy: If the number of teacher A’s enrollment is x, the number of scientific research is y, they can produce (x+1)*y papers at most, using the first x*C time to enroll students and the last y*B time to do scientific research.

Because the K is less than 10001, so we can just enumerate x from 1 to K. Use $y = ceil(K / (x + 1) )$ to find the minimum value of y, while the x determined.

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

int B,C,K;

long long ans = 1000000000;

int main(){
    scanf("%d%d%d", &B, &C, &K);
    for(int x = 0; x <= K; ++x){
        int y = (K+x) / (x+1);
        if(x*C + y*B < ans)
            ans = x*C + y*B;
    }
    printf("%lld\n", ans);
    return 0;
}

3. The date of the scholarship

The range of n is so small that we can calculate it month by month: we know the day of the week on the 1st of the month, then we can calculate the day of the week on the 13th of the month. And then calculate the day of the week on the 1st of the next month based on the number of days in this month.

#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;

int n, day;

int num[13]={0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int cnt[8];

bool isleap(int x){
    if(x%4!=0) return 0;
    if(x%400==0) return 1;
    if(x%100==0) return 0;
    return 1;
}

int main(){
    scanf("%d", &n);
    day = 1; //星期1
    for(int i=1900; i<1900+n; ++i){
        for(int j=1; j<=12; ++j){
            ++cnt[(day + 12 - 1) % 7 + 1];
            if(j == 2){
                if(isleap(i))
                    day = (day + 29 - 1)%7 + 1;
                else
                    day = (day + 28 - 1)%7 + 1;
            }
            else
                day = (day + num[j] - 1)%7 + 1; 
        }
    }
    for(int i=1; i<=7; ++i)
        printf("%d ", cnt[(i + 5 - 1)%7 + 1]);
    return 0;
}

4. Horse traversal

This is a classic breadth-first search problem. Just put the initial position in your queue and start your bfs.

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

const int MAXN = 410;

int n, m, x, y;

int ans[MAXN][MAXN];

int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2 , -1};

struct Point{
    int x, y, d;
} que[MAXN*MAXN], node;

int Head, Tail;

int main(){
    cin>>n>>m>>x>>y;
    for(int i=1; i<=n; ++i)
        for(int j=1; j<=m; ++j)
            ans[i][j] = -1;
    ans[x][y] = 0;
    node.x = x;
    node.y = y;
    node.d = 0;
    que[++Tail] = node;
    int vx, vy;
    while(Head<Tail){
        Point u = que[++Head];
        for(int i=0; i<8; ++i){
            vx = u.x + dx[i];
            vy = u.y + dy[i];
            if(1<=vx && vx<=n && 1<=vy &&vy <=m && ans[vx][vy] == -1){
                ans[vx][vy] = u.d + 1;
                node.x = vx;
                node.y = vy;
                node.d = u.d + 1;
                que[++Tail] = node;
            }
        }
    }
    for(int i=1; i<=n; ++i){
        for(int j=1; j<=m; ++j)
            printf("%d ", ans[i][j]);
        puts("");
    }
}

5. [COCI ‘21 Contest 2 #4] Magneti

problem link: https://dmoj.ca/problem/coci21c2p4

solution link: https://dmoj.ca/problem/coci21c2p4/editorial

Little Marko is bored of playing with shady cryptocurrencies such as Shiba Inu or XRC, which is why he decided to play with magnets. He has $n$ different magnets and a board which has $l$ available empty slots in a row, in which the magnets can be placed. Each pair of adjacent slots is exactly one centimeter apart. Each of the magnets has a radius of activity that is equal to $r_i$. This means that it will attract all magnets that are located strictly less than centimeters away (regardless of the radius of activity of the other magnet). It is possible that some magnets have the same radius of activity, but they are considered as different magnets.

Marko doesn’t like it when the magnets attract each other, so he is interested in the number of ways to place the magnets on the board so that no magnet attracts any other. All of the magnets should be placed on the board, and each empty slot may contain at most one magnet. Two ways of placing the magnets are considered different if there is a magnet which is at a different position in the first way than in the second way. As the required number can be quite large, you should output it modulo $10^9+7$.

$1 \leq n \leq 50$ and $n \leq l \leq 10000$

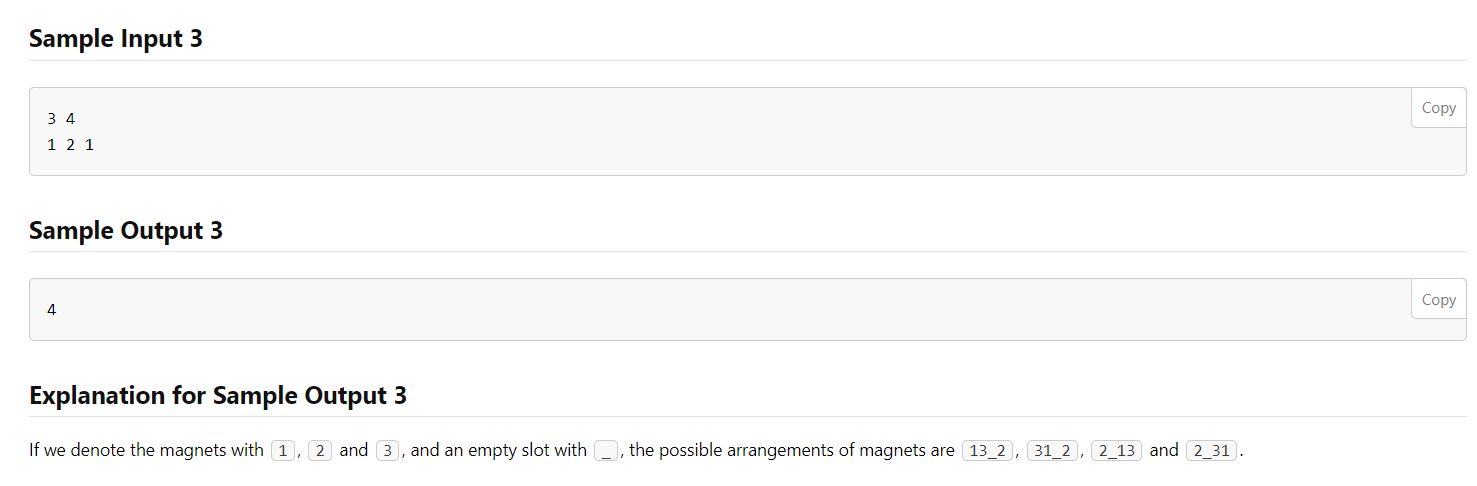
We sort the magnets by increasing radius and build the permutation with the following dp:

dp[i][j][d]: number of ways to arrange the first i magnets in j groups such that the sum of the lengths of the groups is d.

One group represents a segment of the permutation that is being built and is comprised of magnets and the least amount of empty space between them. The transition of the dp actually consists of adding a new magnet to one of the groups, which can be done in three ways:

1. creating a new group that is made just from this magnet
2. adding a magnet to one of the ends of one of the already existing groups
3. connecting two existing groups by placing the new magnet between them

The solution has been explained very clearly in the link, but the state transition equation is not provided.

Here is the state transition equation, which might help you understand:

creating a new group that is made just from this magnet:

$dp[i+1][j+1][d+1] += dp[i][j][d]$

adding a magnet to one of the ends of one of the already existing groups:

$dp[i+1][j][d+r_{i+1}] += dp[i][j][d] \times j \times 2$

connecting two existing groups by placing the new magnet between them:

$dp[i+1][j-1][d + 2 \times r_{i+1} - 1] += 2 \times C^{2}_{j} \times dp[i][j][d]$

The answer is:

$\sum_{d=1}^{l}{dp[n][1][d] \times C_{l-d+n}^{n}}$

boundary condition:

$dp[0][0][0] = 1$

we can find inverse elements with linear complexity:

$P = k * x + r$

$x^{-1} \equiv -\lfloor \frac{P}{i} \rfloor \times r^{-1} \ \ (mod \ P)$

Then preprocess the factorials and their inverse elements.

So we calcuate any combination number within O(1) time.

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio> 

using namespace std;

const int MAXN = 55;
const int MAXL = 10000;
const long long MOD = 1000000007;

int n, l, r[MAXL];
 
long long fac[MAXL+10], inv[MAXL+10], invfac[MAXL+10];

long long dp[MAXN][MAXN][MAXL+10];

long long C(long long n, long long m) {
	if(n < m){
		return 0;
	}
	else{
		return fac[n] * invfac[m] % MOD * invfac[n - m] % MOD;
	}
}

int main(){
	scanf("%d%d", &n, &l);
	for(int i = 1; i <= n; ++i)
		scanf("%d", &r[i]);
		
	fac[0] = 1;
	for(int i = 1; i <= MAXL; ++i)
		fac[i] = fac[i - 1] * i % MOD;
	
	inv[1] = 1;
	for (int i = 2; i <= MAXL; ++i)
		inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;

	invfac[0] = 1;
	for (int i = 1; i <= MAXL; ++i)
		invfac[i] = invfac[i - 1] * inv[i] % MOD;
	
	sort(r + 1, r + n + 1);
	
	dp[0][0][0] = 1;
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= i; ++j){
			for(int d = 1; d <= l; ++d){
				dp[i][j][d] = dp[i - 1][j - 1][d - 1];
				if(d >= r[i]){
					dp[i][j][d] += (dp[i - 1][j][d - r[i]] * j * 2) % MOD;
					dp[i][j][d] %= MOD;
				}
				if(d >= 2 * r[i] - 1){
					dp[i][j][d] += (dp[i - 1][j + 1][d - r[i] * 2 + 1] * j % MOD * (j + 1)) % MOD;
					dp[i][j][d] %= MOD;
				}
			}
		}
	}
	long long ans = 0;
	for(int d = 1; d <= l; ++d){
		ans += dp[n][1][d] * C(l - d + n, n) %MOD;
		ans %= MOD;
	}
	printf("%lld", ans);
	return 0;
}