论文拆解:Understanding the Performance of Sparse Matrix-Vector Multiplication
论文拆解:Understanding the Performance of Sparse Matrix-Vector Multiplication
Abstract
In order to gain an insight on the details of SpMxV performance, we conduct a suite of experiments on a rich set of matrices for three different commodity hardware platforms.
作者通过对三种商品硬件平台,在丰富矩阵集上进行实验,深入了解SpMxV性能的细节。
1. Introduction
一个背景知识:CG and GMRES迭代求解方法需要用到稀疏矩阵向量乘法
介绍了稀疏矩阵向量乘法内存受限的几个原因:
- 相比于$M\times M$和$LU$,矩阵乘向量的计算复杂度为$O(n^2)$,但是内存访问的区域却同样是$O(n^2)$,内存访问相对于浮点计算的比率远大于$M\times M$和$LU$
MxM and LU benefit from the so called surface-to-volume effect, since for a problem size of n they perform O(n^3) operations on O(n^2) amount of data. On the contrary, matrix-vector multiplication performs O(n^2) operations on O(n^2) amount of data, which means that the ratio of memory access to floating point operations is significantly higher.
数据的重用很少,即时间局部性受限
Seen from another point of view, there is little data reuse in the matrix-vector multiplication, i.e. very restricted temporal locality.
稀疏矩阵的存储结构使性能进一步下降
When sparsity comes into play, the performance is further degraded.
一个一般的结论:可以利用有关矩阵结构和处理器架构特征的信息来有效地优化SpMxV
A general conclusion is that SpMxV can be efficiently optimized by exploiting information regarding the matrix structure and the processor’s architectural characteristics.
简单介绍先前研究
概括先前研究存在的不足:
先前的研究主要关注已报告问题的一个子集,对有限数量的稀疏矩阵进行优化。这可能会导致与之前各种工作中使用的CPU相互矛盾的结论,甚至可能导致对SpMxV优化的问题和候选解决方案的混淆。
In general, previous research focuses on a subset of the reported problems
and proposes optimizations applied to a limited number of sparse matrices. This fact, along with the CPUs used in various previous works, may lead to contradictory conclusions and, perhaps, to confusion regarding the problems and candidate solutions for SpMxV optimization.很少有人研究应用所提出的优化后性能提升的确切原因。
In addition, the exact reason for performance gain after the application
of the proposed optimizations is rarely investigated.
列举了两个例子:阻塞方法提高性能的原因尚不清楚,缺乏局部性是否是SpMxV中的一个关键问题
简单介绍本文研究的目的:帮助理解SpMxV在现代微处理器上的性能问题。
The goal of this paper is to assist in understanding the performance issues of SpMxV on modern microprocessors.
指出这项研究的创新性:目前没有关于SpMxV内核或其任何优化版本在当前的微架构上的性能行为的实验结果。
To our knowledge, there are no experimental results concerning the performance behavior of this kernel, or any of its optimized versions, on current microarchitectures.
简要介绍研究方法和成果:对文献中报道的算法问题进行了分类。对于每个问题,在从Tim Davis的收藏中选择的100个矩阵上,进行一系列实验,以量化其对性能的影响。实验结果为SpMxV在现代微处理器上的性能提供了宝贵的见解,并揭示了在优化过程中可能特别有用的问题。
In order to achieve this goal, we have categorized the problems of the algorithm as reported in literature. For each problem we conduct a series of experiments in order to quantify its effect on performance. Our experimental results provide valuable insight on the performance of SpMxV on modern microprocessors and reveal issues that will probably prove particularly useful in the process of optimization. Our experiments are performed on a large suite of 100 matrices selected from Tim Davis’ collection [4]. Based on the conclusions drawn from the conducted experiments, we propose guidelines that can aid the optimization process.
指出下文的组织结构:
第2节:介绍了有关SpMxV和优化方法的相关工作
第3节:介绍了基本算法和报告的问题
第4节:展示了各种实验结果,阐明了SpMxV的性能问题
第5节:总结了结论并讨论了未来的研究工作
The rest of the paper is organized as follows: Section 2 presents related work on SpMxV and optimization methods and Section 3 presents the basic algorithm and the reported problems. In Section 4 we present various experimental results that illuminate the performance issues of SpMxV,
while Section 5 summarizes our conclusions and discusses future research work.
2. Related work
总结二十年来对于稀疏矩阵向量乘法的研究
Sparse matrix-vector multiplication has attracted intensive scientific attention in the last two decades.
概括这些研究存在的不足:
(a) 实验评估中使用的矩阵套件通常很小
(b) 评估平台在大多数情况下包括上一代微架构
(c) 结论有时相互矛盾
(d) 所提出的方法所获得的性能提升没有针对所攻击的特定问题进行彻底分析
Summarizing on the results of previous research on the field, the following conclusions may be drawn: (a) the matrix suites used in the experimental evaluations are usually quite small, (b) the evaluation platforms include in most cases previous generation microarchitectures, (c) the conclusions are sometimes contradictory and (d) the performance gains attained by the proposed methods are not thoroughly analyzed in relevance to the specific problems attacked.
由此引出本文研究的目标:这项工作的目标是了解SpMxV内核在现代微处理器上的性能问题并提供可靠的优化指南。为此,我们采用了100个矩阵,进行了各种各样的实验,并报告了从微处理器提供的性能监控设施收集的性能数据和信息。
The goal of this work is to understand the performance issues of SpMxV kernel on modern microprocessors and provide solid optimization guidelines. For this reason we employ a wide suite of 100 matrices, perform a large variety of experiments and report performance data and information collected from the performance monitoring facilities provided by the microprocessors.
3. Basic algorithm and problems
简要介绍了CSR存储格式:
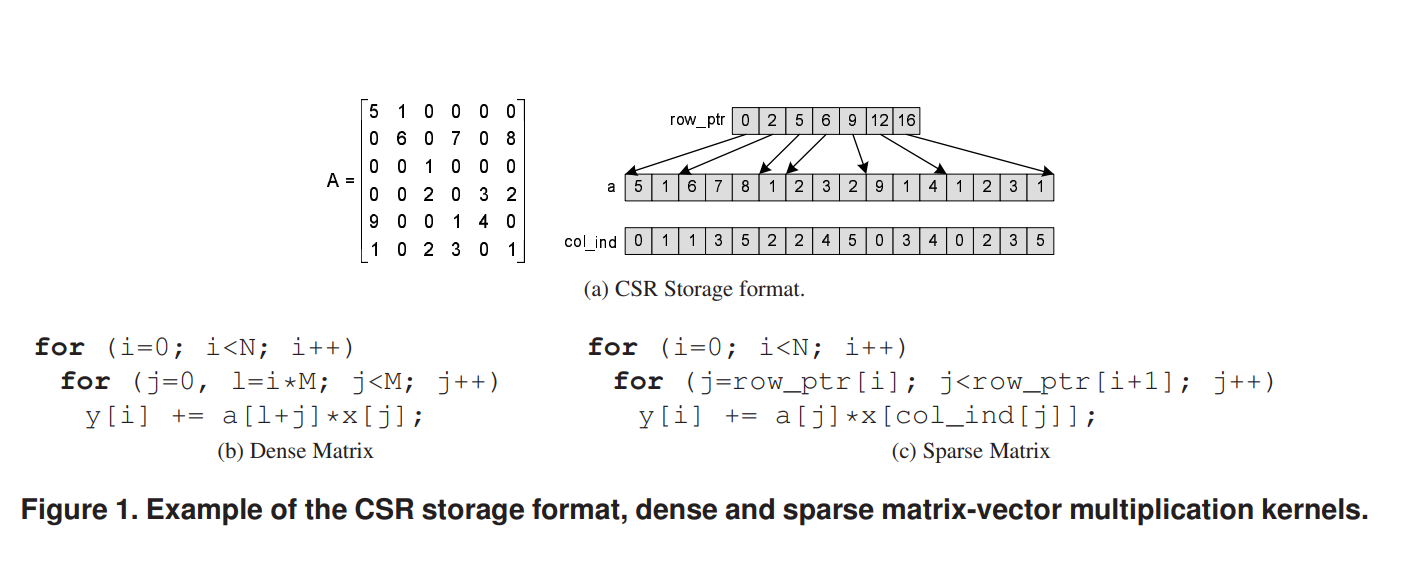
我个人的理解:这种存储方式类似于图论中把邻接矩阵存储为邻接链表,用n个行指针指向矩阵每一行的第一个非零元素,同时存储每个元素的值和列号
根据文献,列出可能影响其性能的问题:
According to literature, SpMxV presents the following problems that can potentially affect its performance:
内存强度(矩阵中没有时间局部性)。这是算法中固有的问题,无论矩阵是稀疏的还是密集的。与其他重要的数值程序(如矩阵乘法(MxM)或LU分解)不同,SpMxV内核受内存限制,因为矩阵向量乘法中的矩阵元素仅使用一次。
间接内存引用。例如CSR存储格式需要通过col ind和row ptr数据结构存储和访问矩阵元素的索引。这一事实意味着额外的加载操作、内存子系统的流量和缓存干扰。
向量x的不规则内存访问。与密集矩阵中对向量x的访问顺序不同,在稀疏矩阵中,这种访问是不规则的,并且依赖于矩阵的稀疏结构。这一事实使得利用向量x访问中固有的重用性的过程变得复杂。
行长较短:尽管这个问题并不明显,但在实践中经常遇到。许多稀疏矩阵都表现出大量长度较短的行。当内循环的行程数较少时,这一事实可能会由于循环的大量开销而降低性能。
4. Experimental evaluation
4.1 Experimental preliminaries
实验准备:
介绍了使用的100个矩阵集合:
#1 是一个密集的 1000×1000 矩阵
#2-45 是在SPARSITY中被使用的矩阵
#46 是一个 10000×10000 随机稀疏矩阵
#87 是一个由SPARSKIT创建的5点模板有限差分矩阵
其余的都是集合中非零元素数量和行数最大的矩形矩阵
大部分矩阵是从Tim Davis的集合中选出的,所有矩阵都以CSR格式存储
接下来介绍了实验平台用到的三种微处理器:
Intel Core 2 Xeon(时钟速度:2.6GHz,4MB L2 缓存 – Woodcrest)
Intel Pentium 4 Xeon(时钟速度:2.8GHz,1MB L2 缓存 – Netburst)
AMD Opteron(时钟速度:1.8GHz,1MB L2 缓存 – Opteron)
操作系统、编译器信息:
Linux (kernel version 2.6) for the x86 64 ISA
gcc version 4.1 with the -O3 -funroll-loops optimization flags
性能测试的具体方法和评估指标:
The experiments were conducted by measuring the execution time of 128 consecutive SpMxV operations with randomly created x vectors for every matrix in the set and for each different microprocessor. The floating point operations per second (FLOPS) metric of each run was calculated by dividing the total number of operations (2×nnz) by the execution time. We used 64-bit integers for the representation of indices in col ind and applied double precision arithmetic. It should be noted that we made no attempt to artificially pollute the cache after each iteration, in order to better simulate iterative scientific application behavior, where the data of the matrices are present in the cache, either because they have just been produced, or because they were recently accessed.
简单介绍硬件预取,并测试硬件预取对Intel处理器SpMxV内核性能的影响:
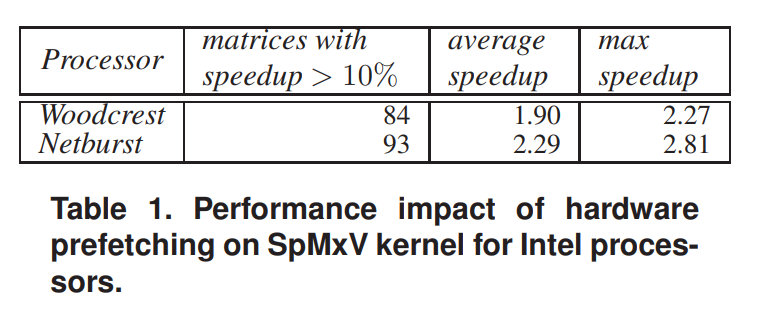
图表显示,在两个Intel处理器上,开启硬件预取,对于SpMxV内核性能都有提升,大部分矩阵在运算时加速了10%以上。在Netburst处理器上的性能提升效果比Woodcrest处理器好。
4.2 Experimental evaluation of serial SpMxV
先测试了SpMx的基本性能作为对照,之后分别针对上文提出的三个稀疏矩阵特有的问题设计了比较实验
4.2.1 Basic performance of serial SpMx
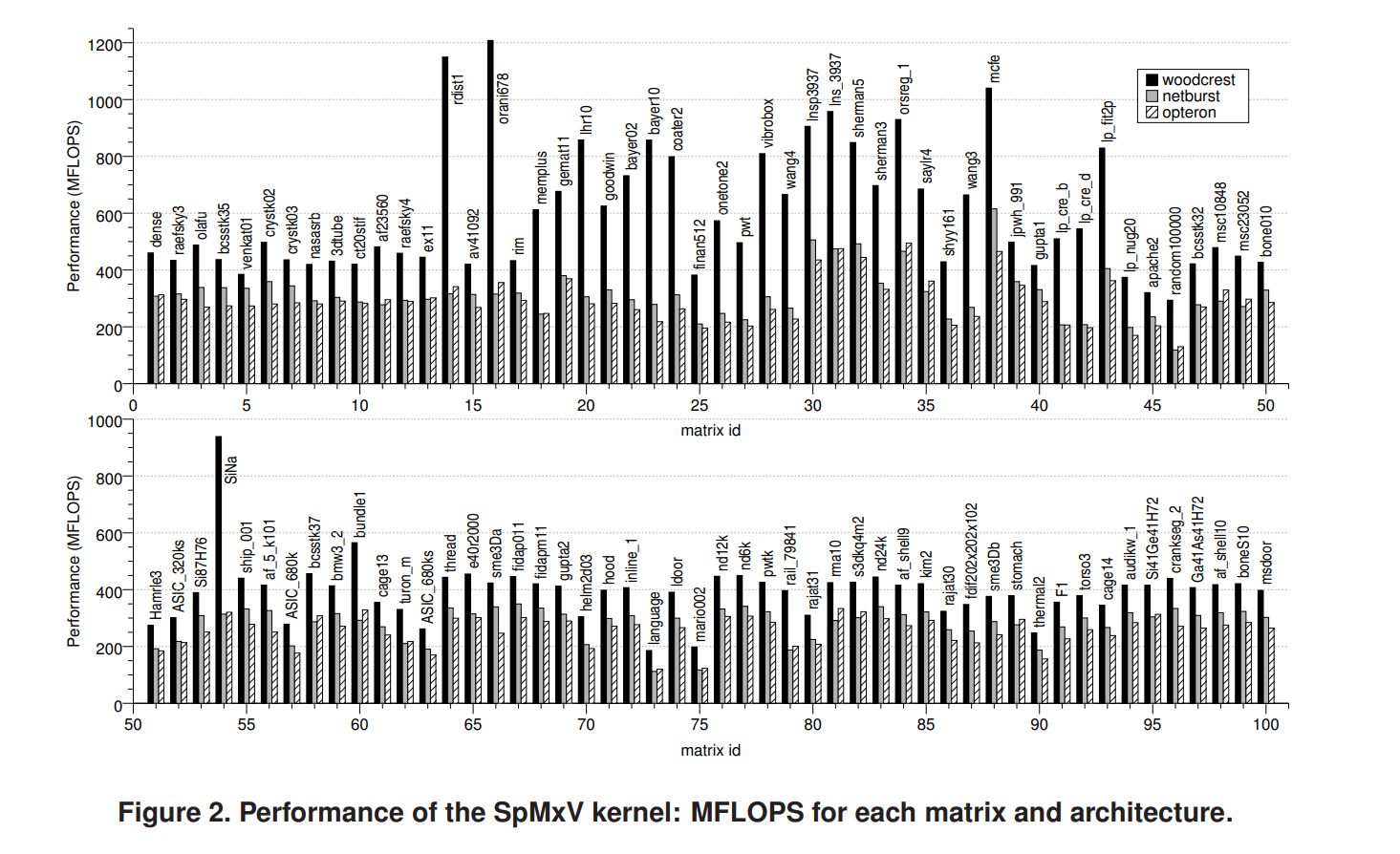
图2显示了实验集上每个矩阵和架构的SpMxV内核的详细性能结果(以 FLOPS 为单位)
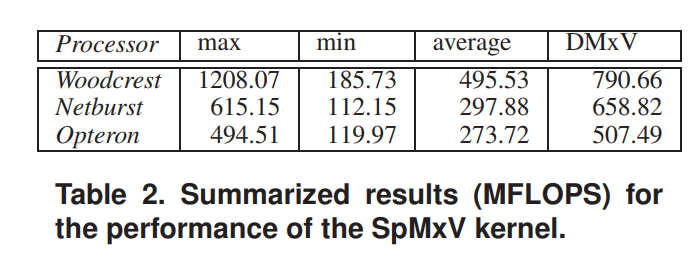
表格2显示了SpMxV内核在不同架构的处理器上的综合性能
根据图2可以看出,在矩阵集里面不同矩阵上的性能具有很大的差异。为了进一步阐述这一观察结果,我们把矩阵集区分为两个不同的类别:工作集完全适合L2缓存的矩阵,因此只会出现强制未命中;工作集大于L2缓存大小的矩阵,可能会出现容量未命中。工作集 (ws) 的计算公式为:ws = (nnz × 2 + nrows × 2 + ncols) × 8。
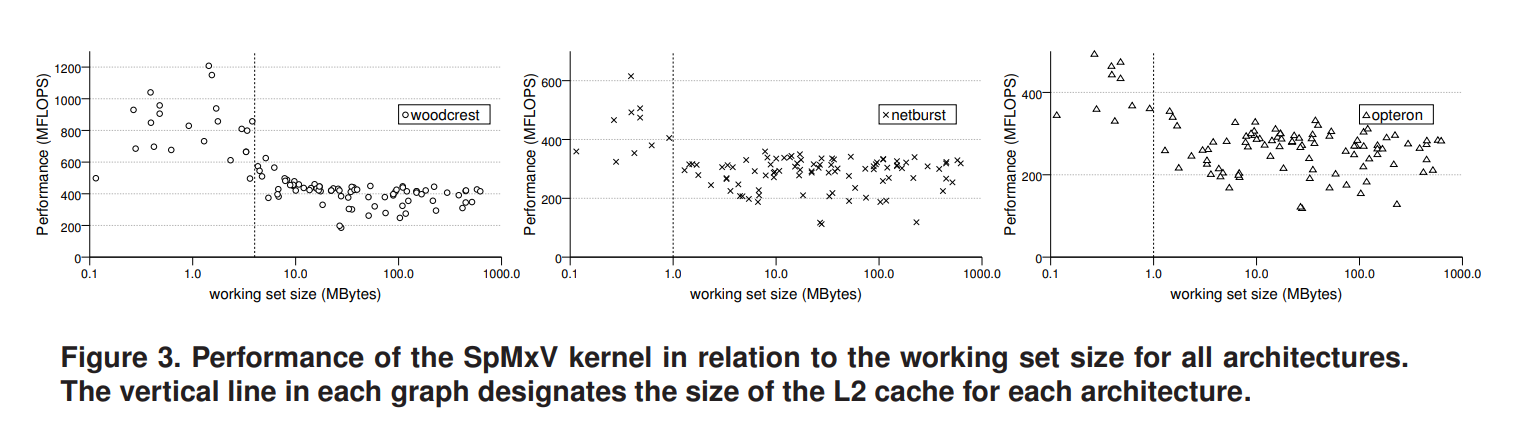
在图3中,我们展示了每个矩阵所达到的性能,其工作集标记为x轴。每个图中的垂直线表示每个架构的L2缓存大小。该图表明,各种矩阵性能之间的巨大差异是由于其工作集的大小造成的。如果矩阵的工作集小于缓存,则预期性能会显著提高。
这两个类别所涉及的性能问题都不同,比较不同类别的矩阵的性能可能会导致错误的结论。
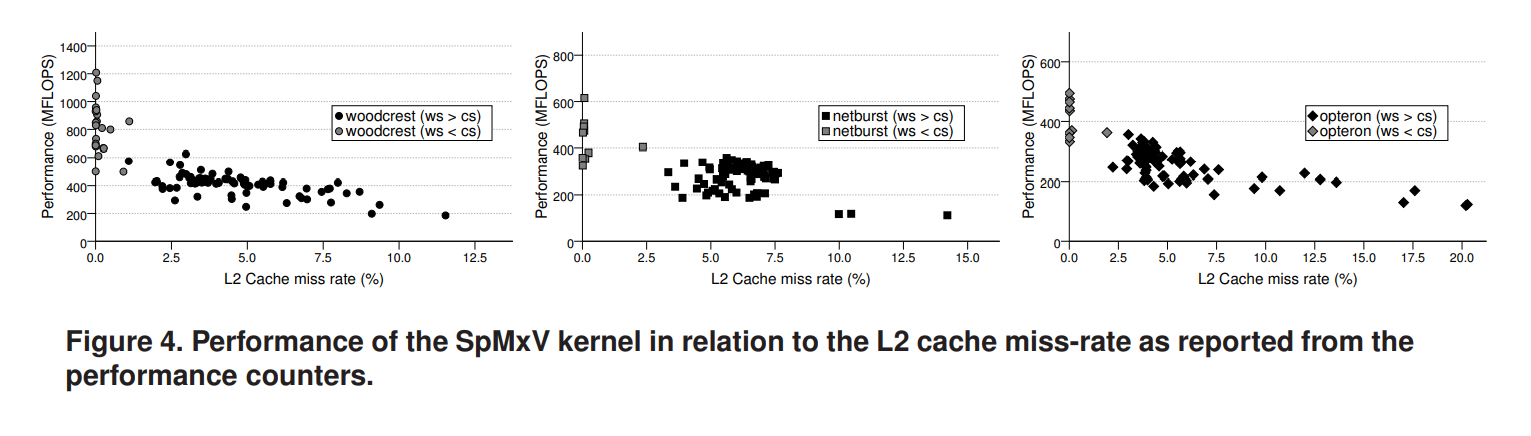
图4展示了每个矩阵相对于L2缓存未命中率的性能,该性能是根据每个处理器的性能计数器测量的。正如预期的那样,小于缓存大小的工作集表现出接近于零的L2未命中率。在更粗略的层面上,FLOPS中的性能和L2未命中之间似乎存在相关性。但是仅靠L2未命中率指标不足以了解内核的性能。例如,某些具有相似未命中率的矩阵的MFLOPS差异很大。
4.2.2 Irregular accesses
noxmiss benchmark:将col ind数组清零,以便对x的每个引用都只访问x[0],使得对x的访问模式几乎完美。忽略掉计算数值上的不同对性能造成的影响,只考虑不规则的访问对性能的影响。
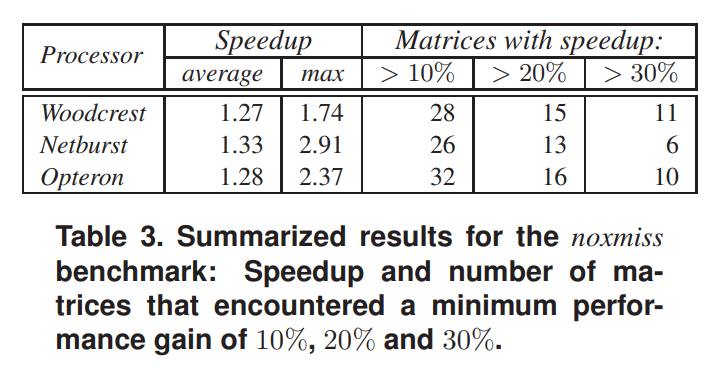
只有一小部分矩阵(不超过整个矩阵集的1/3)在所有处理器上都实现了超过10%的显著性能加速。这意味着SpMxV的不规则访问模式不是主要的性能问题。
对于绝大多数矩阵,对x的访问似乎呈现出一些规律,这些规律要么有利于从缓存中重用数据,要么表现出可被硬件预取机制检测到的模式。然而,在标准基准测试中表现较差的大多数矩阵在 noxmiss 基准测试中遇到了相当显著的加速。
通过这个现象可以得出这样的结论:存在一个矩阵子集,其中对x的不规则访问对性能造成了相当大的阻碍。这些矩阵具有相当不规则的非零元素模式,最终导致对x的访问不佳和重用率低,从而降低性能。
4.2.3 Short row lengths
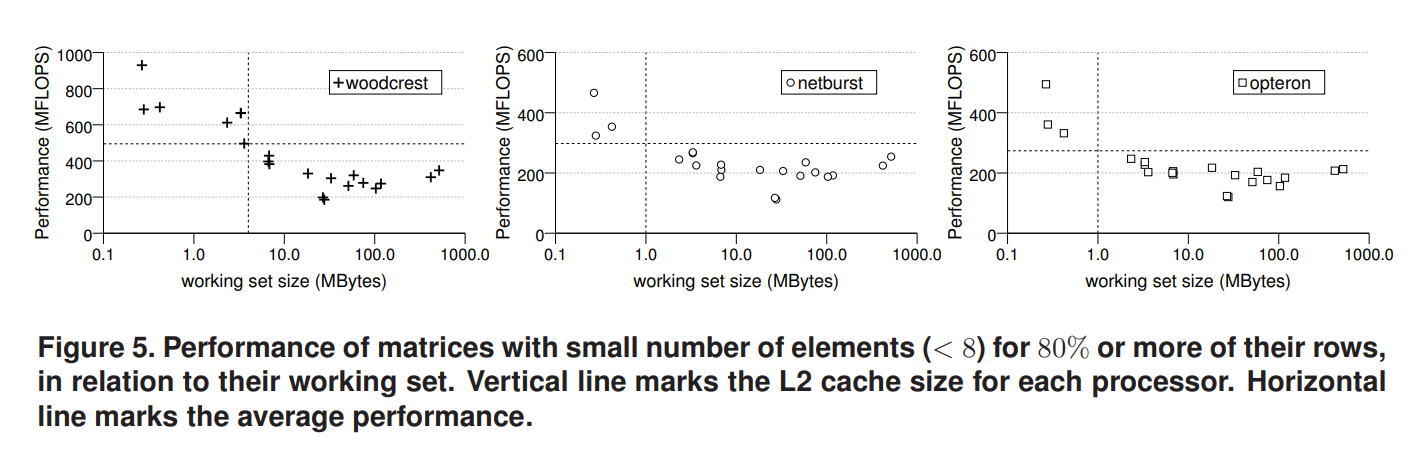
图5是把超过80%的行包含少于八个元素的矩阵单独拿出来得到性能相对于工作集大小的分布图,图中水平虚线是所有矩阵的平均性能。可以看出具有较大工作集和许多短行的矩阵表现出的性能明显低于平均值。然而,具有许多短行和小工作集的矩阵实现了非常好的性能,这一事实暗示循环开销不是唯一的因素。
支持上述观点的另一个重要观察结果是,图5中报告的矩阵与应用noxmiss基准测试时受益的矩阵一致(几乎没有例外)。这些事实引导我们得出结论:短行长可能代表x向量的大量缓存未命中。这可以通过以下事实来解释:短行长增加了在后续行中访问x的完全不同元素的可能性。
4.2.4 Indirect memory references
noind-rowptr,noindcolind benchmark:使用了每行具有恒定数量的连续元素的合成矩阵。这些矩阵使我们能够通过用顺序访问来消除两种间接访问
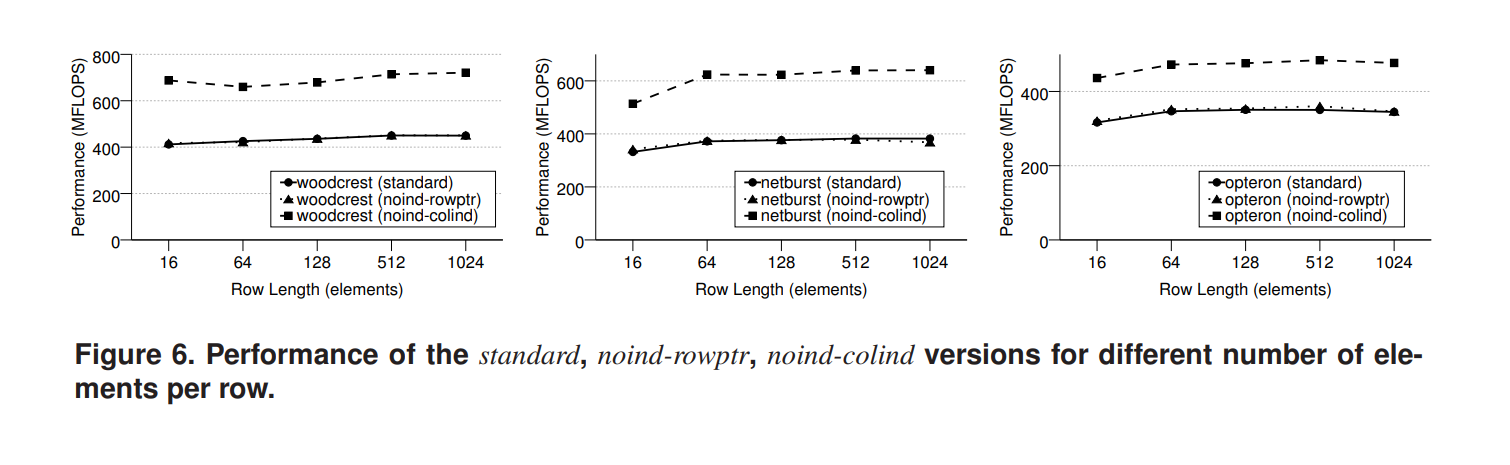
图6可以明显看出,row ptr中的间接内存引用不会影响性能。这是可以预见的,因为这些引用很少,并且取代了内部循环初始化中已经存在的开销。另一方面,通过col ind间接访问x的开销会导致性能急剧下降。在这种情况下,x的每次内存访问都会被一次额外的内存访问所累加,这会增加问题的ws,在代码中添加额外的指令并限制内核的IPC。
4.2.5 Memory intensity (no temporal locality in the matrix)
进行了一组简单的比较实验:我们使用32位而不是64位整数作为col ind结构,以减少工作集的总大小。Woodcrest的加速比为1.20,Netburst的加速比为 1.29,Opteron的加速比为1.17。令人印象深刻的是,ws降低了22.4%,同时性能显著提高了。根据这些结果,我们可以得出结论,在间接内存访问的情况下观察到的改进主要是由于ws的减少。

此外,内核在表示矩阵的数据结构a、col ind和row ptr中没有表现出重用,传统上认为缺乏时间局部性会影响性能。然而,如图1所示,所有上述结构都以非常规则的流式模式和单位步长进行访问。硬件预取器能够检测这些简单的访问模式并透明地从内存中获取其相应的缓存行。因此可以得出一个相当可靠的结论:矩阵中缺乏时间局部性导致缓存未命中的情况非常少,因此性能不会受到这一特定因素的影响。
4.3 Conclusions on the experiments and optimization guidelines
通过上述实验可以得到一些结论:
内核的性能受矩阵工作集的影响非常大。但是由于工作集小的矩阵对应于小规模的问题,因此它们的优化意义不大,我们专注于工作集大于L2缓存的大型工作集矩阵。此外,减少同一问题的ws会释放内存总线资源,使执行速度显着提高。
算法的内存强度以及间接内存引用对x的影响是SpMxV性能不佳的最关键因素,并影响所有矩阵。
x访问的不规则性和许多短行的存在在较小范围内影响性能。
矩阵结构缺乏时间局部性不会通过可以优化的问题(例如缓存未命中)影响性能,但本质上会增加内存访问次数。
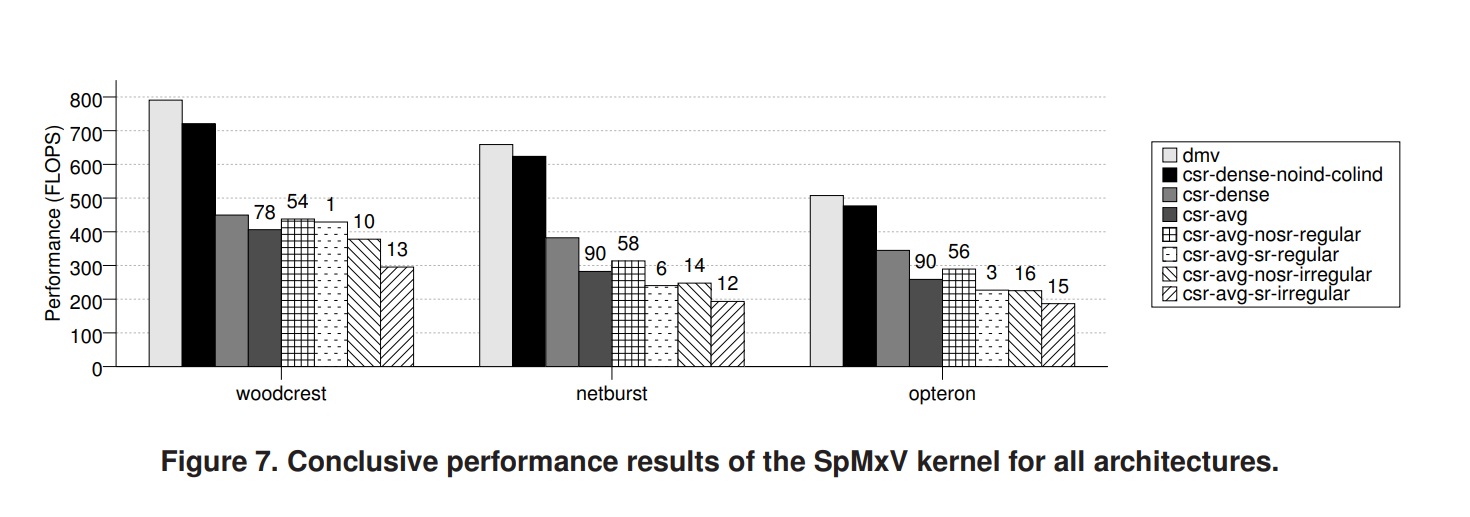
图7是对结果的统计分析,前三个条形图表示密集矩阵(1024 × 1024)以密集格式(dmv)存储和以csr格式存储的标准情况(csrdense)和noind-colind基准(csr-dense-noindcolind)的矩阵向量乘法性能。csr-avg(?)表示矩阵集合中所有工作集大于L2大小的矩阵的平均性能,而其余的条形图则对应于这些矩阵的所有可能子集,这些子集基于它们的规律性(-irregular/-regular)以及它们是否以短行为主(-sr/-nosr)
原文中的一个小问题:
原文此处疑似是指csr-avg,出现了笔误?
首先,从csr-dense-nocolind到csr-dense之间接近2倍的性能差异,是col ind的间接引用导致的
另外,如果矩阵表现出一些不良特征,例如不规则性和许多短行,则性能可能会进一步下降约1.35倍。另一方面,如果矩阵不以短行为主并以规则方式访问x,则其性能可能会比平均水平提高1.1倍,并接近存储在CSR中的密集矩阵的性能。还要注意,大多数矩阵都是不以短行为主并以规则方式访问x。
由此总结出以下优化原则:
- 通过使用尽可能小的数据类型(例如,col ind使用32位或16位整数,x使用单精度存储)来减小ws大小,以减少内存子系统的压力。即使牺牲CPU周期来减小ws大小(例如,通过应用压缩)也会使性能提高。增加ws的存储结构成功的机会很小。
Reduce the ws size by using the smallest possible data types (e.g. 32-bit or 16-bit integers for col ind, single precision storage for x) in order to reduce the pressure on the memory subsystem. Even sacrificing CPU cycles to reduce the ws size (e.g. by applying compression) will also lead to performance improvement (as in [21]). Storage structures that increase the ws have small opportunities to succeed.
- 减少间接内存引用。这可以通过利用矩阵中的常规结构来实现,例如全对角线或密集子块。
Reduce indirect memory referencing. This could be achieved by exploiting regular structures within the matrix such as full diagonals (as in [1]) or dense sub-blocks (e.g. BCSR format as in [3, 8, 19]).
- 谨慎填充。添加许多非零元素来实现优化方法可能会极大地影响性能,主要是由于ws的增加。额外的浮点运算不会造成这么大的问题,因为CPU有空闲周期。
Pad sparingly. Adding many non-zero elements to accomplish an optimization approach may dramatically affect performance, mainly due to the increase in the ws. The extra floating-point operations should not create such a big problem, since the CPU has idle cycles to spare. Thus, the BCSR format used in [3, 8, 19] is expected to be beneficial only in the subset of matrices that contain many dense subblocks.
- 注意行长较短和循环开销。一些优化方法将矩阵拆分为子矩阵的总和。在这种情况下,应注意子矩阵不要属于行长较短的矩阵类别。如果在乘法内核中插入额外的外循环,也可能产生大量开销,尤其是在行短的矩阵中。
Beware of short row lengths and loop overheads. Some optimization approaches split the matrix into a sum of submatrices (as in [1,19]). In this case one should take care that the submatrices do not fall into the category of matrices with short row lengths. Alternatively, one may insert an additional outer loop in the multiplication kernel (as in [13]). This may also incur significant overheads especially in matrices with short rows.
- 识别x向量上存在访问问题的矩阵,仅对它们应用缓存重用优化。
Identify matrices with problematic access on the x vector and apply cache reuse optimizations only to them.
- 只要CPU支持硬件预取,就无需应用软件预取来解决缺乏时间局部性的问题。
There is no need to apply software prefetching to attack the problem of the lack of temporal locality as long as the CPU supports hardware prefetching.
5. Conclusions – Future work
这项研究的结论和意义:得到了有关现代微处理器架构上稀疏矩阵向量乘法的性能问题的大量实验结果,阐明并量化了所报告问题对内核性能的影响,并有助于制定优化代码的指南。
In this paper we presented extensive experimental results regarding the performance issues of sparse matrixvector multiplication on modern microprocessor architectures. Our results illuminate and quantify the effect of the reported problems on the kernel’s performance and can aid in forming a guideline to optimize the code.
指出未来工作的方向:我们将应用从本文中获得的知识,使用短矢量化方法优化内核,我们相信这将通过减少工作集、间接引用以及利用矢量内存负载和浮点运算来提供性能优势。
For future work, we will apply the knowledge gained from this paper in order to optimize the kernel using a short vectorization approach, which we believe that will provide performance benefits from the reduction of the working set, the indirect referencing and from the utilization of vector memory loads and floating-point operations.